Como desenhar um triângulo equilátero numa circunferência com a ajuda de um compasso e de uma régua?

O compasso é um instrumento que serve para traçar circunferências e arcos de circunferência e para comparar e transportar medidas.

De um lado temos uma ponta metálica chamada ponta seca, do outro uma mina de grafite que deve estar sempre bem afiada e à mesma altura da ponta seca.


Como desenhar um triângulo equilátero numa circunferência com a ajuda de um compasso e  de uma régua?

Marca no papel um ponto C. 
Pega o compasso e com a ponta seca no ponto C, traça uma circunferência com o raio que desejares.

Passo 2

Pega uma régua e traça um diâmetro da circunferência, marcando os pontos A e B. Não te esqueças,  o diâmetro é o segmento de reta que une dois pontos da circunferência passando pelo centro C.

Passo 3

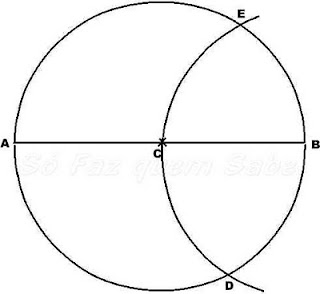
Pega o compasso novamente, abre-o com uma abertura igual ao raio da circunferência que  traçaste, ou seja, medida da abertura igual a AC ou BC. Com centro em B (coloca a ponta seca do compasso no ponto B), traça um arco que intersecte a circunferência nos dois pontos D e E.

Passo 4

Pronto, os pontos A, D e E dividem a circunferência em três partes iguais, ou seja, os arcos AE, ED e DA são congruentes (tem a mesma medida).

 Como esses arcos são congruentes, as cordas AE, ED e DA da circunferência, também são congruentes. Logo, os pontos A, D e E são os vértices de um triângulo equilátero (os três lados tem  medidas iguais).

Portanto, ao pegar o lápis e a régua e unir o ponto A ao ponto E; o ponto E ao ponto D e o ponto D ao ponto A  estarás desenhando o triângulo equilátero inscrito na circunferência.

 

 Da reunião dos pontos AED surge um polígono inscrito na circunferência de nome "TRIÂNGULO EQUILÁTERO".



Vamos um pouco mais além e se dividirmos a circunferência  em quatro triângulos  congruentes:


Divisão da circunferência em quatro partes iguais:



1 - Traça a circunferência  com diâmetro AB.

2 - Com o auxílio do compasso e com centro em B, traça um arco de circunferência em cima e outro em baixo com uma abertura superior a metade do diâmetro.

3 - Agora e fazendo centro em A e, com a mesma abertura, traça dois arcos de circunferência um em cima e outro em baixo que cruzem os anteriores e encontrem os pontos D e C.

4 - Com o auxílio da régua une os pontos A C, C B, B D, e D A, obtêm-se a divisão da circunferência em quatro partes iguais.

5 - Da reunião dos pontos ABCD surge um polígono inscrito na circunferência de nome "QUADRADO" em que:

 o comprimento de AD=comprimento de DB=comprimento de DC=comprimento de CA.