Noção de ângulo. Ângulos convexos e concâvos. Ângulos adjacentes.Ângulos geometricamente iguais

Já alguma vez leste um livro, ou viste um filme onde se procuram tesouros?

Imagina que tu  és um desses exploradores. 

"Anda 10 passos e vira 90º para a direita. Anda mais 5 passos e vira outra vez 90º para a direita. Anda mais 10 passos e vira 90º à direita. Volta a andar mais 5 passos e vira mais 90º para a tua direita." 

Surpreendido? Verifica, num papel qual a tua posição.

Para poderes responder a este desafio deves saber de que estamos a falar de  ângulos e  graus.

O ângulo é uma região do plano composta pela abertura de duas semirretas que possuem uma origem em comum, chamada vértice do ângulo.

 A abertura do ângulo é medida em graus, a que damos o nome de amplitude.

Ângulo é a abertura formada entre duas semirretas de mesma origem. Vejamos:

Para medirmos a amplitude de um ângulo utilizamos um objeto chamado de transferidor.

Observa que um dos lados do ângulo aponta para a medida 0º e a outra para a medida 50º, portanto o ângulo é agudo e mede 50º.
 

Nesse caso, um dos lados do ângulo está voltado para 0º e outro para 90º, dessa forma, o ângulo mede 90º e é denominado reto.

Um dos lados aponta para a medida 0º e o outro para a medida 120º, portanto, o ângulo é obtuso, medindo 120º.


Toda medição de ângulos deve ocorrer como foi demonstrado, um dos lados fica apontado para o zero e outro lado apontará para a medida da abertura do ângulo. O vértice dos ângulos, que é o local onde as semirretas se originam, deve ficar no centro da base do transferidor.

Tipos de ângulos

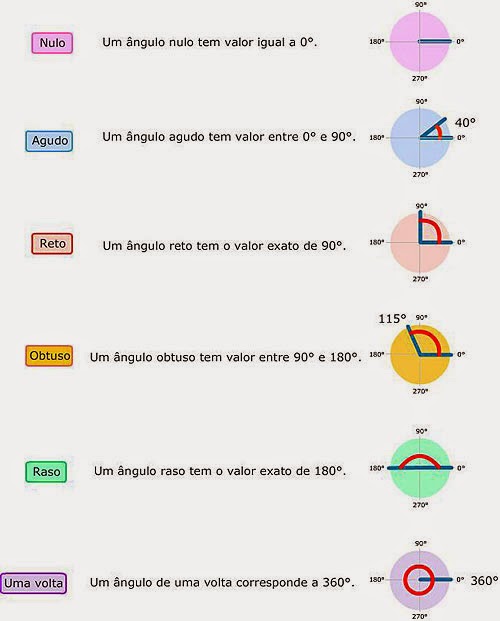
De acordo com a amplitude de cada ângulo podemos classificá-lo como:

• Ângulo raso: tem de amplitude 180º.

• Ângulo obtuso:  tem uma amplitude compreendida entre 90º e 180º.

• Ângulo reto:  tem uma amplitude de 90º.

•  Ângulo agudo: Ângulo cuja amplitude é maior do que 0° e menor do que 90°.

•   Ângulo giro que  tem de amplitude 360º.

 RESUMINDO:

Relações entre ângulos

- ÂNGULOS ADJACENTES: 

Dois ângulos são ângulos adjacentes quando têm em comum o vértice e um dos lados e nenhum outro ponto.

Os ângulos AOB e BOC são adjacentes

São ângulos adjacentes

os ângulos: DBA e CBD.

NOTA: São ângulos não adjacentes (sem lados comuns)

os ângulos: EBA e CBD.

NOTA: São ângulos não adjacentes (com um lado comum)

os ângulos: DBA e EBA.

- ÂNGULOS GEOMETRICAMENTE IGUAIS: 

Dois ângulos  são geometricamente iguais se tiverem a mesma amplitude  ou quando sobrepostos coincidem um com o outro, ponto por ponto.

Vejamos um exemplo:

RELEMBRA QUE:



A Mediatriz de um segmento de reta é uma reta que lhe é perpendicular e passa pelo seu ponto médio. Todos os pontos da mediatriz de um segmento de reta estão igualmente distantes  dos extremos dos segmentos.

A Bissectriz de um ângulo é a semirreta com origem no vértice  do ângulo A e que o divide em dois outros  ângulos congruentes  ou geometricamente iguais.