Classificação dos triângulos, desigualdade triangular

O triângulo é uma das formas geométricas mais importantes no estudo da geometria e é bastante utilizado em construções.

 O Triângulo é o polígono com o menor número de lados (3 lados) e a soma dos seus ângulos internos é  sempre igual a 180^o.

102º + 44º + 34º = 180º










Os triângulos podem ser classificados de acordo com as medidas de seus lados e de acordo com as medidas de seus ângulos internos. Vejamos como isso ocorre.



Primeiro, vamos classificar os triângulos quanto aos lados. 

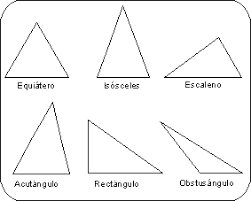
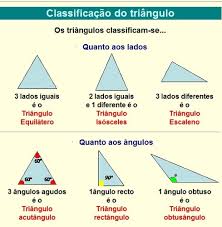
Quanto aos lados o triângulo pode ser: Equilátero, Isósceles ou Escaleno.

1. Classificação quanto aos lados

Triângulo Equilátero: é todo triângulo que apresenta os três lados com a mesma medida. Nesse caso dizemos que os três lados são congruentes.

Triângulo Isósceles: é todo triângulo que apresenta dois lados com a mesma medida, ou seja, dois lados de tamanhos iguais.

Triângulo Escaleno: é todo triângulo que apresenta os três lados com medidas diferentes, ou seja, três lados de tamanhos diferentes.

 Segundo, vamos classificar quanto aos ângulos internos.

O triângulo pode ser: acutângulo, obtusângulo ou retângulo.

2. Classificação quanto aos ângulos

Triângulo acutângulo: é todo triângulo que apresenta os três ângulos internos menores que 90^o, ou seja, os três ângulos internos são agudos.

Triângulo obtusângulo: é todo triângulo que apresenta um ângulo interno maior que 90^o, ou seja, que possui um ângulo obtuso.

Triângulo retângulo: é todo triângulo que apresenta um ângulo interno reto, ou seja, que possui um ângulo medindo 90^o.

Resumindo:

Será que é sempre possível   construir um triângulo dados os comprimentos dos três lados?    Observa as imagens (medidas em cm).

Concluímos que  num triângulo o comprimento de qualquer lado é menor que a soma dos outros dois.

Em qualquer triângulo a soma do comprimento de dois lados é maior que o comprimento do terceiro lado. Esta propriedade chama-se DESIGUALDADE TRIANGULAR.

a + c > b ou b < a + c

Por exemplo, sendo 2,5 cm  e  7,5 cm  os comprimentos de dois lados de um triângulo, o terceiro lado varia entre  5  e  10 cm excluindo o 5 e o 10 , porque:

                2,5 + 7,5 = 10 cm

                7,5 - 2,5 = 5 cm

Exemplos:

Desigualdade triangular:

A Érica decidiu fazer no seu jardim um canteiro em forma de triângulo. Pensou construí-lo com os seguintes comprimentos: 10 metros, 2 metros e 7 metros. Será que a Érica pode construir esse canteiro? 

Relembra a Desigualdade triangular: 
Num triângulo o comprimento de qualquer lado é  sempre menor que a soma dos outros dois lados. 

Assim, 10 > 2+7. Conclui-se então que a Erica não pode construir o canteiro com essas medidas.

Ângulos internos e externos de um triângulo

 Calcula as amplitudes dos ângulos desconhecidos ( x, y, z ), da figura:

ângulo Y= 180º-60º= 120º

ângulo Z= 180º - 120º= 60º

ângulo X= 180 - (60º+60º)= 60º



Para praticares já, é só clicares:

Exercício de aplicação de ângulos e triângulos