Um bom ano 2013!!!

Mediatriz de um segmento de reta e Bissectriz de um ângulo

 A Mediatriz de um segmento de reta é uma reta que lhe é perpendicular e passa pelo seu ponto médio. Todos os pontos da mediatriz de um segmento de reta estão igualmente distantes  dos extremos dos segmentos.







 A Bissectriz de um ângulo é a semirreta com origem no vértice  do ângulo A e que o divide em dois outros  ângulos congruentes  ou geometricamente iguais.

Como desenhar um triângulo equilátero numa circunferência com a ajuda de um compasso e de uma régua?

O compasso é um instrumento que serve para traçar circunferências e arcos de circunferência e para comparar e transportar medidas.

De um lado temos uma ponta metálica chamada ponta seca, do outro uma mina de grafite que deve estar sempre bem afiada e à mesma altura da ponta seca.


Como desenhar um triângulo equilátero numa circunferência com a ajuda de um compasso e  de uma régua?

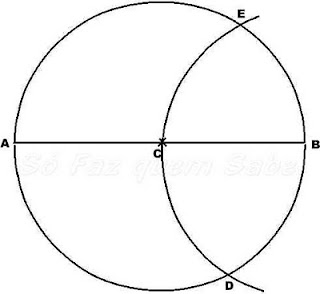
Marca no papel um ponto C. 
Pega o compasso e com a ponta seca no ponto C, traça uma circunferência com o raio que desejares.

Passo 2

Pega uma régua e traça um diâmetro da circunferência, marcando os pontos A e B. Não te esqueças,  o diâmetro é o segmento de reta que une dois pontos da circunferência passando pelo centro C.

Passo 3

Pega o compasso novamente, abre-o com uma abertura igual ao raio da circunferência que  traçaste, ou seja, medida da abertura igual a AC ou BC. Com centro em B (coloca a ponta seca do compasso no ponto B), traça um arco que intersecte a circunferência nos dois pontos D e E.

Passo 4

Pronto, os pontos A, D e E dividem a circunferência em três partes iguais, ou seja, os arcos AE, ED e DA são congruentes (tem a mesma medida).

 Como esses arcos são congruentes, as cordas AE, ED e DA da circunferência, também são congruentes. Logo, os pontos A, D e E são os vértices de um triângulo equilátero (os três lados tem  medidas iguais).

Portanto, ao pegar o lápis e a régua e unir o ponto A ao ponto E; o ponto E ao ponto D e o ponto D ao ponto A  estarás desenhando o triângulo equilátero inscrito na circunferência.

 

 Da reunião dos pontos AED surge um polígono inscrito na circunferência de nome "TRIÂNGULO EQUILÁTERO".



Vamos um pouco mais além e se dividirmos a circunferência  em quatro triângulos  congruentes:


Divisão da circunferência em quatro partes iguais:



1 - Traça a circunferência  com diâmetro AB.

2 - Com o auxílio do compasso e com centro em B, traça um arco de circunferência em cima e outro em baixo com uma abertura superior a metade do diâmetro.

3 - Agora e fazendo centro em A e, com a mesma abertura, traça dois arcos de circunferência um em cima e outro em baixo que cruzem os anteriores e encontrem os pontos D e C.

4 - Com o auxílio da régua une os pontos A C, C B, B D, e D A, obtêm-se a divisão da circunferência em quatro partes iguais.

5 - Da reunião dos pontos ABCD surge um polígono inscrito na circunferência de nome "QUADRADO" em que:

 o comprimento de AD=comprimento de DB=comprimento de DC=comprimento de CA.



Circunferência e círculo, corda, raio e diâmetro

A circunferência é uma figura que possui o formato circular e está presente em diversas situações relacionadas ao nosso dia a dia.

Se observares atentamente à tua volta, verificas que o formato circular é muito importante para o funcionamento perfeito de alguns objectos.

 Por exemplo, as rodas de um carro possuem o formato circular, o que facilita a sua locomoção. 

 As rodas de uma bicicleta, a tampa de uma panela, algumas placas de trânsito, entre outros objectos, possuem formato circular.

No desporto também  podes observar a presença do formato circular:

Por exemplo,  o centro do campo de futebol  é delimitado por uma circunferência.

Será que também  confundes circunferência com círculo?  

O círculo é a parte interna da circunferência.

A circunferência é a linha que limita o círculo.

RAIO: Raio de uma circunferência (ou de um círculo) é um segmento de recta com uma extremidade no centro da circunferência e a outra extremidade num ponto qualquer da circunferência. 

Na figura, os segmentos de recta OA, OB e OC são raios.

CORDA: Corda de uma circunferência é um segmento de recta cujas extremidades pertencem à circunferência.
 Na figura, os segmentos de recta AC e DE são cordas.

DIÂMETRO: Diâmetro de uma circunferência (ou de um círculo) é uma corda que passa pelo centro da circunferência. Observamos que o diâmetro é a maior corda da circunferência.  
  Na figura, o segmento de recta AC é um diâmetro.

Preparação para a ficha de avaliação de Novembro....revisões

Para teres sucesso no teste de 28 de Novembro de 2012 terás que saber:

- Identificar retas, segmentos de retas e semirretas;
- Identificar segmentos de retas paralelas, perpendiculares, obliquas com a notação adequada;
-Utilizar o transferidor, para ver a amplitude de um ângulo;
-Traçar ângulos com a régua e o transferidor;
-Identificar ângulos retos, obtusos e agudos;
-Classificar triângulos quanto aos lados (equilátero, isósceles, escaleno) e quanto à amplitude (rectângulo, acutângulo e obtusângulo);
-Desenhar triângulos isósceles e equiláteros;
-Calcular o perímetro de polígonos (sabendo que o perímetro é a soma de todos os comprimentos dos lados) e identificar o comprimento dos lados dos triângulos;
-Identificar ângulos complementares, suplementares, adjacentes, verticalmente opostos;
-Calcular a amplitude de um ângulo do triângulo, conhecendo as outras amplitudes (sabendo que a soma dos ângulos internos de um triângulo é sempre 180º;
-Identificar os sólidos geométricos (poliedros e não poliedros): prismas, pirâmides, cones, cilindro;
-Ter uma noção do que são os sólidos platónicos (sabendo que todas as faces são polígonos congruentes/iguais);
-Classificar os sólidos geométricos em relação ao número de faces, arestas, vértices;
-Conhecer e aplicar a Relação de Euler  (F + V = A + 2 ou   F + V – A = 2)
                                                                       F= nº de faces
                                                                       V= nº de vertíces
                                                                       A= nº de arestas

Ângulos e triângulos

from Helena Borralho


Figuras no plano ( retas, ângulos e triângulos)

from Helena Borralho

sólidos geométricos

from Helena Borralho

Polígonos 

 from Helena Borralho



Para praticares, é só clicares:

Exercícios sobre retas, semirretas e segmentos de reta

Exercício sobre ângulos e triângulos

Construção de triangulos

construção de triângulos

Como usar o transferidor para medir ângulos?

 from Andrea Reinoso

Classificação dos triângulos, desigualdade triangular

O triângulo é uma das formas geométricas mais importantes no estudo da geometria e é bastante utilizado em construções.

 O Triângulo é o polígono com o menor número de lados (3 lados) e a soma dos seus ângulos internos é  sempre igual a 180^o.

102º + 44º + 34º = 180º










Os triângulos podem ser classificados de acordo com as medidas de seus lados e de acordo com as medidas de seus ângulos internos. Vejamos como isso ocorre.



Primeiro, vamos classificar os triângulos quanto aos lados. 

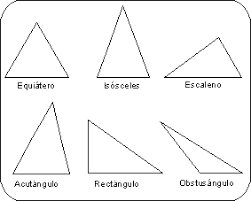
Quanto aos lados o triângulo pode ser: Equilátero, Isósceles ou Escaleno.

1. Classificação quanto aos lados

Triângulo Equilátero: é todo triângulo que apresenta os três lados com a mesma medida. Nesse caso dizemos que os três lados são congruentes.

Triângulo Isósceles: é todo triângulo que apresenta dois lados com a mesma medida, ou seja, dois lados de tamanhos iguais.

Triângulo Escaleno: é todo triângulo que apresenta os três lados com medidas diferentes, ou seja, três lados de tamanhos diferentes.

 Segundo, vamos classificar quanto aos ângulos internos.

O triângulo pode ser: acutângulo, obtusângulo ou retângulo.

2. Classificação quanto aos ângulos

Triângulo acutângulo: é todo triângulo que apresenta os três ângulos internos menores que 90^o, ou seja, os três ângulos internos são agudos.

Triângulo obtusângulo: é todo triângulo que apresenta um ângulo interno maior que 90^o, ou seja, que possui um ângulo obtuso.

Triângulo retângulo: é todo triângulo que apresenta um ângulo interno reto, ou seja, que possui um ângulo medindo 90^o.

Resumindo:

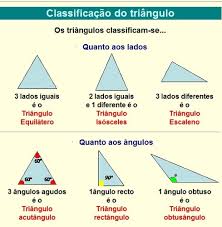
Será que é sempre possível   construir um triângulo dados os comprimentos dos três lados?    Observa as imagens (medidas em cm).

Concluímos que  num triângulo o comprimento de qualquer lado é menor que a soma dos outros dois.

Em qualquer triângulo a soma do comprimento de dois lados é maior que o comprimento do terceiro lado. Esta propriedade chama-se DESIGUALDADE TRIANGULAR.

a + c > b ou b < a + c

Por exemplo, sendo 2,5 cm  e  7,5 cm  os comprimentos de dois lados de um triângulo, o terceiro lado varia entre  5  e  10 cm excluindo o 5 e o 10 , porque:

                2,5 + 7,5 = 10 cm

                7,5 - 2,5 = 5 cm

Exemplos:

Desigualdade triangular:

A Érica decidiu fazer no seu jardim um canteiro em forma de triângulo. Pensou construí-lo com os seguintes comprimentos: 10 metros, 2 metros e 7 metros. Será que a Érica pode construir esse canteiro? 

Relembra a Desigualdade triangular: 
Num triângulo o comprimento de qualquer lado é  sempre menor que a soma dos outros dois lados. 

Assim, 10 > 2+7. Conclui-se então que a Erica não pode construir o canteiro com essas medidas.

Ângulos internos e externos de um triângulo

 Calcula as amplitudes dos ângulos desconhecidos ( x, y, z ), da figura:

ângulo Y= 180º-60º= 120º

ângulo Z= 180º - 120º= 60º

ângulo X= 180 - (60º+60º)= 60º



Para praticares já, é só clicares:

Exercício de aplicação de ângulos e triângulos

Ângulos complementares e suplementares, ângulos verticalmente opostos e ângulos alternos internos e externos

Dois ângulos são complementares, quando a  soma de suas amplitudes for igual a 90º.

Dois ângulos  são suplementares se a soma das suas amplitudes for igual a 180º.

 

Dois ângulos dizem-se verticalmente opostos se têm o mesmo vértice e os lados de um ângulo estão no prolongamento dos lados do outro.

Assim,

O ângulo AOC e o ângulo DOB são verticalmente opostos.

O ângulo AOB e o ângulo COD são verticalmente opostos.

Resumindo, os ângulos verticalmente opostos são geometricamente iguais.

Ângulos alternos-externos 

 Num sistema de duas rectas paralelas cortadas por  uma  terceira,  chamada  secante,  chamam-se  ângulos  alternos-externos  aos pares a,c e b,d assinalados na figura.

Os  ângulos  alternos-externos  são  geometricamente iguais, por isso  têm a mesma amplitude; a amplitude de a é igual à de c, o mesmo sucedendo entre b e d.



Ângulos alternos-internos 

Num sistema de duas rectas paralelas cortadas por uma terceira chamam-se ângulos alternos-internos aos pares e, g e f, h assinalados na figura.

Os ângulos alternos-internos são geometricamente iguais, por isso têm a mesma amplitude; a amplitude de e é igual à de g, o mesmo sucedendo entre f e h.

Por isso,  concluimos que os Ângulos alternos Externos  são geometricamente iguais e os os Ângulos alternos internos também  são geometricamente iguais.






Exemplos:

Para cada uma das situações seguintes, indica a amplitude dos ângulos representados por letras.

a) Ângulos Complementares - Dois ângulos dizem-se complementares quando a sua soma é 90º.

X= 90º-35º = 55º

b) Ângulos Suplementares - Dois ângulos dizem-se complementares quando a sua soma é 180º.

X= 180º - 145º = 35º

c) Ângulos verticalmente opostos - os ângulos verticalmente opostos  têm a mesma amplitude.

X= (360º - 25 -25) :2=

X= 310 :2 = 155º

Como traçar retas paralelas e perpendiculares?

Como traçar retas from ArmindaOliveira

Ângulos, vértices e bissectriz

Já alguma vez leste um livro, ou viste um filme onde se procuram tesouros?

Imagina que tu  és um desses exploradores. 

"Anda 10 passos e vira 90º para a direita. Anda mais 5 passos e vira outra vez 90º para a direita. Anda mais 10 passos e vira 90º à direita. Volta a andar mais 5 passos e vira mais 90º para a tua direita." 

Surpreendido? Verifica, num papel qual a tua posição.

Para poderes responder a este desafio deves saber de que estamos a falar de  ângulos e  graus.

O ângulo é uma região do plano composta pela abertura de duas semirretas que possuem uma origem em comum, chamada vértice do ângulo.
 A abertura do ângulo é medida em graus, a que damos o nome de amplitude.

Num polígono qualquer, como os que podes ver mais abaixo, podemos ter dois tipos de ângulo, os internos a verde e os externos a vermelho.

Resumindo, Um ângulo é um conjunto de pontos, e o vértice e os lados do ângulo fazem parte desse conjunto.

Um ângulo divide o plano em duas partes não limitadas.   
 -  C  é o vértice do ângulo ACB (a origem comum das semirretas que formam um ângulo chama-se vértice do ângulo ).

 -   As semirretas  ĊB  e  ĊA  são os lados do ângulo ACB

                                       

A bissectriz de um ângulo divide o ângulo em duas partes iguais.

ĊV  é a bissectriz do ∢ACB.

Os  ∢ACV  e  ∢VCB  são geometricamente iguais.

Nota que: ∢ = ângulo

Tipos de ângulos

De acordo com a amplitude de cada ângulo podemos classificá-lo como:

A-Ângulo reto quando  a sua medida é igual  a  90º.

Nota:  Estas duas retas concorrentes de ângulos adjacentes também se chamam de retas PERPENDICULARES.

 B- Ângulo  agudo  quando  a sua medida é menor que a medida de um ângulo reto de 90°. 

Exemplo:

 



C-Ângulo obtuso  quando  a sua medida é maior que a medida de um ângulo reto de 90°  e menor que um ângulo de 180º. 

Exemplo:

D- Ângulo raso  quando  a sua medida é igual  a  180°.

        

Concluindo:

• Ângulo raso: tem de amplitude 180º.

• Ângulo obtuso:  tem uma amplitude compreendida entre 90º e 180º.

• Ângulo reto:  tem uma amplitude de 90º.

•  Ângulo agudo: Ângulo cuja amplitude é maior do que 0° e menor do que 90°.

Também existe o  Ângulo giro que  tem de amplitude 360º.