Conversões, adições e subtrações de medidas de amplitude

Quando, usando o transferidor, medes a amplitude de um ângulo,utilizas o grau como unidade de medida.

O grau divide-se em duas subunidades: minuto e segundo.


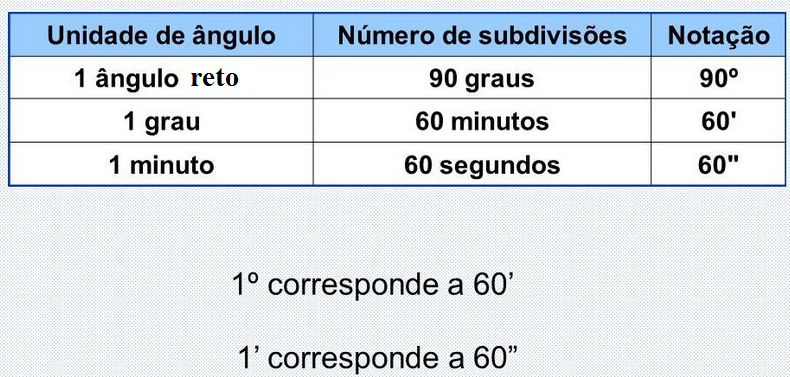
Um grau corresponde a 60 minutos (de grau)         1º= 60 ´
Um  minuto corresponde a 60 segundos (de grau)   1'= 60 ´´

Exemplo 1:

 Um ângulo tem 4º35´de medida de amplitude.
Como indicar, em minutos, a medida de amplitude desse ângulo?

Sabendo que  1º= 60 ´ então  4º= 4 x 60´=240´

logo 4º35´= 240´+35´= 275´


Resposta:  4º 35 =  275´



Exemplo 2:

Como transformar em graus, minutos e segundos as seguintes medidas de amplitude ?

·         Transforme 130' em graus e minutos.

•        Transforme 150'' em minutos e segundos.

       

•   Transforme 26 138'' em graus, minutos e segundos.

Vejamos, este exemplo mais pormenorizadamente:

26 138''= 435´38" = 7º 15´38"

• Transforme 23 716''  em graus, minutos e segundos.

Como  60'' = 1' , vamos ver quantos minutos tem 23716 segundos.

23716'' : 60'' = 395'  resto 16''  (São 395 minutos e 16 segundos)



Vejamos agora, quantos graus são 395 minutos sabendo que  60´ = 1º

395' : 60' = 6º  resto 35'


Vejamos, este exemplo mais pormenorizadamente:

 23 716'' = 395' 16'' = 6º 35' 16''

outros exemplos:

·         Transforma 30º em minutos.

Solução

Sendo 1º = 60', temos:

                30º = 30 . 60'= 1.800

'Logo, 30º = 1.800
   

·         Transforme 5º35' em minutos.

Solução

                5º = 5 . 60' = 300'

                300' +  35'= 335'

Logo, 5º35'= 335'.
   

·         transforma 8º em segundos.

Solução

Sendo 1º = 60', temos:

               8º = 8 . 60'= 480

'Sendo 1'= 60'', temos:

                480'= 480 . 60'' = 28.800''

Logo, 8º = 28.800''.

   

·         Transforma 3º35' em segundos.

Solução

                3º = 3 . 60'= 180'

                180' +  35' = 215'

                215' .  60''  = 12.900''

Logo, 3º35'= 12.900''

·         Transforma 2º20'40'' em segundos.

Solução

                 2º = 2 . 60' = 120'

                 120' + 20'  = 140'

                  140'. 60''= 8.400''

                  8.400'' + 40'' = 8.440''

Logo, 2º20'40'' = 8.440''

Os ângulos podem ser somados, multiplicados, subtraídos e divididos. 
Para fazer isso, no entanto, é necessário levar em conta uma característica específica: suas sub-unidades são os minutos e os segundos.
 E muitas vezes é necessário fazer  transformações com medidas de ângulos durante essas operações.

Quando se efetua uma soma de números decimais e quando a soma das unidades chega a dez ou mais, "coloca-se 1" à casa das dezenas.

O mesmo vale para as dezenas (" e vai 1" na casa das centenas), e assim por diante.

No caso dos ângulos é a mesma coisa: quando os minutos chegarem a 60 ou mais, adiciona-se "1" na casa dos graus.




Adição de medidas de amplitudes de ângulos

exemplo:  16º  18'  32'' 
               + 7º  55'  30'' 
               = 23º 73'  62'' 

 mas como o minuto e o segundo só podem atingir os 60, temos de reduzir 73' em graus e minutos e o 62'' em minutos e segundos.

73' = 1º13' 
 62''=1'2''

logo, 23º 73'  62'' =   24º 14' 2''
Resposta:  24º 14' 2''


. Subtração de medidas de amplitudes de ângulos

exemplo: 28º  3'   24''
              - 8º  15'  30''

Não podemos subtrair o subtrativo pois os minutos e os segundos são superiores aos do aditivo. Assim temos que transformar o primeiro para aumentar o valor dos minutos e segundos.

Tiramos ao 28º um grau e fica 27º. 

Adicionamos 60 minutos que equivale ao grau que tirámos.

Já temos 27º 63' 24''.

Agora para alterar os segundos tiramos um minuto e passámo-lo para segundos, ou seja, adicionar 60 segundos.
Fica   27º  62'   84''

Agora já podemos fazer a subtração. 
27º  62'    84''
-8º   15'   30''
19º   47   54''

Resposta: 19º  47' 54''



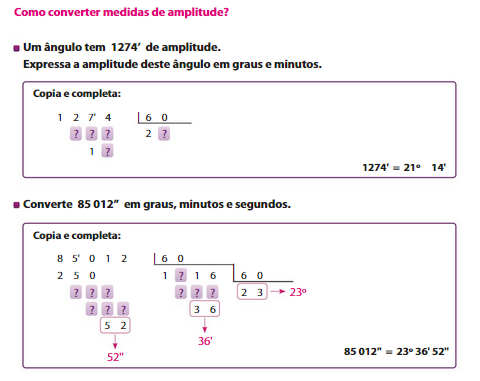
LEMBRA-TE QUE: